RIP Benoit Mandelbrot

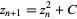
Benoit Mandelbrot was a British mathematician best known for his work on fractal geometry; he died yesterday at the age of 85. A fractal is a shape that becomes more and more complex the closer you look at it. The most famous example is the Mandelbrot Set, a shape of infinite complexity defined by a simple equation: , where C is the set of complex numbers; if Z in this relation does not tend toward infinity, the number is in the set. The more you magnify this fabulous shape, the more detail you see.

The most interesting real-world consequence of fractal geometry is that the length of a line depends on the scale at which you measure it. If you measure the coastline of Britain on a world map, you get one number, but as you look at the coast on maps of higher resolution you see more and more small features -- inlets, peninsulas, rocks -- that you missed in the global view, and the length of the coastline keeps getting longer. Mandelbrot pointed this out in a famous article titled, "How long is the coastline of Britain?" In my experience it is impossible to persuade even most archaeologists that this is true; people want something like the length of the Mississippi River or the surface area of a person's skin to be a number that is independent of the scale of your map or the length of your ruler. But the world is not like that. As Mandelbrot told the NY Times a few years ago,

Here is a question, a staple of grade-school geometry that, if you think about it, is impossible. The length of the coastline, in a sense, is infinite.

Mandelbrot had a knack for getting the attention of people who had only a little interest in math, and it is typical that the equation to which he put his name is not only mathematically interesting but gorgeous.